Paraboloide hiperbólico

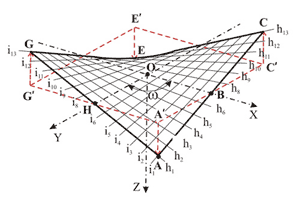
Se llama paraboloide hiperbólico a esta superficie representada según dos puntos de vista distintos en la figura: en una dirección (en el plano y = 0) presenta el aspecto de una parábola orientada hacia arriba de ecuación

y en otra dirección perpendicular (en el plano x = 0) la de una parábola orientada hacia abajo de ecuación

Las secciones por planos horizontales son hipérbolas como queda representado en la figura abajo.

Lo que las curvas cónicas (la elipse, la parábola y la hipérbola) son para la dimensión dos, en dimensión tres lo son las superficies cuádricas. Los nombres de estas superficies tienen que ver con las curvas que aparecen como secciones con planos. En el paraboloide hiperbólico, una de las superficies cuádricas, estas secciones son parábolas e hipérbolas.

El paraboloide hiperbólico, aun siendo una superficie curvada, se puede construir con líneas rectas. Lo único que se tiene que hacer es ir variando el ángulo de inclinación de una recta que se mueve encima de otra curva.

Gaudí fue uno de los que emplearon esta superficie en Arquitectura, pero quien más la ha trabajado ha sido Félix Candela. El mejor ejemplo se puede encontrar en el Restaurante Los Manantiales (1958) en Xochimilco en la ciudad de México. El techo está formado por ocho paraboloides hiperbólicos. La misma estructura se puede encontrar ahora en el nuevo Oceanogràfic (2002) en Valencia.

Tanto Gaudí como Candela aprovecharon superficies matemáticas previamente definidas y estudiadas, con unas ecuaciones perfectamente determinadas y una manera de construirlas totalmente establecida. La única variación permitida consiste en jugar con diferentes valores de los parámetros.